作者: 时间:2024-09-30
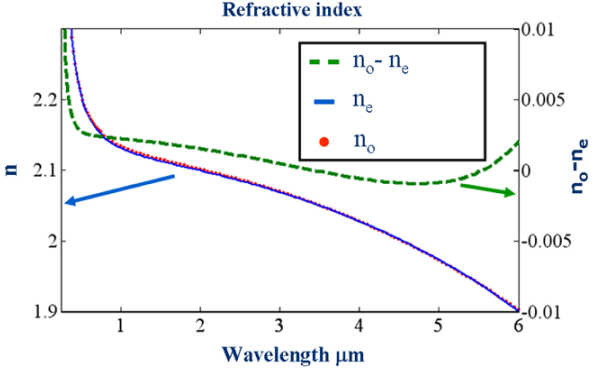
I. Dolev等人在其文章《Linear and nonlinear optical properties of MgO:LiTaO3》发表了相关结果。他们对掺杂0.5% MgO 的化学计量LiTaO3 晶体的非常光和寻常光折射率导出了新的温度相关的的Sellmeier方程。掺杂0.5% MgO 的化学计量LiTaO3 晶体简称PPMgSLT。这个方程是基于准相位匹配频率转换测量,以及热膨胀和热辐射的干涉测量。从室温到200°C,这些方程适用于宽光谱范围,非常光为0.35-6um,寻常光为0.375-3.75um。非线性光学测量为二阶电极化张量的非线性系数d33、d22和d24元素分别设定了12.9、1.54和0.46pm/V的下限值。干涉测量的线性和二次热膨胀系数分别为1.45762e-5 1/°C和2.68608e-8(1/°C)2。Sellmeier方程与以前发表的数据相符。
周期性极化钽酸锂(PPSLT)是一种广泛应用于非线性光学领域的晶体,因为它具有较宽的透明度范围(0.27-6 微米)、较大的非线性系数和较高的抗光学损伤能力。化学计量LiTaO3(SLT)晶体现已上市,与同成分钽酸锂不同,SLT具有较低的矫顽电场,这有利于使用电场极化技术对较厚的样品进行极化,从而实现准相位匹配 (QPM) 频率转换应用 。由于最高非线性极化率张量元d33,最常用的相互作用是e-ee,其中两个非常波会引起非常规的非线性极化。此外,SLT晶体属于三方晶系3m(C3υ),因此,其二阶电极化张量χ(2) 有几个额外的非零元素。这些元素允许另外三种类型的非线性相互作用:O-OO(d22,d21,d16), e-OO (d31, d32)和o-eo (d24, d15)。例如,在 o-eo 相互作用中,寻常波和非常波产生普通二次谐波。对于 e-ee 相互作用,只需要非常光折射率ne(λ,T),但对于其他相互作用,则需要寻常光折射率no(λ,T),以用于非线性过程的精确建模和优化。
近期寻常光折射率no(λ,T)被用于另一种三方3m晶体(LiNbO3)的QPM实验中,其中基波和二次谐波都是寻常波(o-oo,d22)。在实现二阶级联过程时,提出了寻常光指数和非常光折射率的应用,在量子信息应用中,o-eo相互作用可以用于实现多体连续变量纠缠。因此,以0.0001的精度了解SLT的寻常光和非常光偏振的折射率色散方程(Sellmeier方程)是必不可少的。
SLT的Sellmeier方程是根据几篇著作得到的。Nakamura等人和Juvalta等人在室温下,在0.44-1.05um和275-500nm的光谱范围内,分别获得了含ne(λ,T)和no(λ,T)的Sellmeier方程。Abedin等人在0.4-4um的光谱范围和25-300°C的温度范围内,推导了ne(λ,T)和no(λ,T)的Sellmeier方程。Bruner等人在光谱范围为0.39-4.1um、温度范围为30-200°C的范围内,导出了ne(λ,T)的Sellmeier方程。Kolev等人将后者的光谱范围进一步扩展到中红外线,均采用QPM测量技术。虽然上述工作涵盖了大多数应用的大部分温度和光谱范围,但迄今为止所获得的数据还不足以用于非线性光学器件的设计,特别是那些同时涉及ne(λ,T)和no(λ,T)器件。例如, Saltie等人显示了理论方程和实验测量之间的差异。
在本文中,我们提出了适用于广泛的光谱和热范围的Sellmeier方程。我们通过测量与周期性极化晶体相关的非线性相互作用来获得Sellmeier方程,涉及普通极化、非常规极化和普通和非常规极化。我们的测量还使我们能够通过非线性频率转换测量获得x(2)张量元素d33、d22、d24和d32的绝对和相对值。此外,我们通过精确的干涉测量确定了材料的温度膨胀和热色散。
文章采用的实验装置主要分为三个部分:
第一部分是用于检测热膨胀和色散的装置。对于毫米级的样品的线性热膨胀的测量使用到一台单独的激光干涉仪作为光学标准,相同的样品发生光程(厚度)变化时, FP温度扫描干涉法会记录下变化,所有装置都是在真空下运行以排除空气影响。温度测试范围从-150℃到300℃。还用一款改进的干涉仪方案,使用MZ干涉装置优化方案
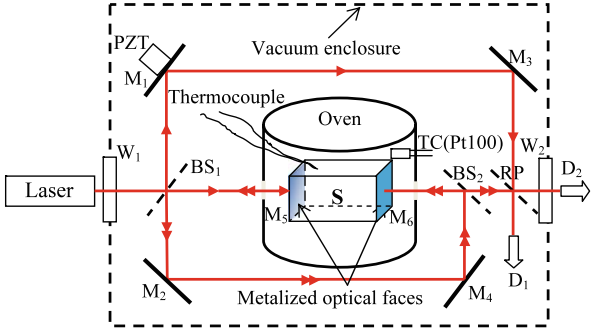
第二部分是Sellmeier方程推导。SLT晶体用Czochraski法生长。准备好SLT晶体后可以进行测量实验。两种非线性匹配模式都要测量:二次谐波和差频发生,通过OPO光学参量振荡器提供,简言之,在二次谐波装置中,使用四种基本光源:可调的0.7-0.9μm钛蓝宝石激光器,1064nm的Nd:YAG激光器,1.5-4.1μm的OPO,1.52-1.62μm的可调谐半导体激光器,用EDFA放大输出,每个光源的测量都控制偏振,用合适的探测器与偏振器测输出的二次谐波。将PPSLT晶体置于温度范围25-200℃的环境下。再一个实验装置是基于PPSLT OPO的下转换,OPO被1.0475μm的Nd:YLF调Q激光器泵浦,发生信号波长在1.4-1.6μm,闲频光波长范围在3.3-4.1μm,为了获取期待的信号光和闲频光的波长,PPSLT晶体放置在温度范围25-200℃的烘箱中,只有非常光的相互作用才能足够有效的超过OPO的阈值条件。二次谐波和OPO的非线性相互作用包含2个波长或3个波长混合,而且满足基本条件,能量守恒和动量守恒。
第三部分是二阶电极化张量的元素测量。使用连续可调的半导体激光器对SLT晶体的二阶电极化张量求解,使用如下方程进行推导。
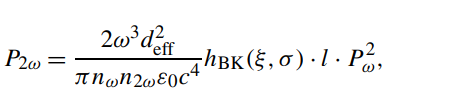
上述方程中,ω和2ω是基频和二次谐波的角频率,ξ和σ是自聚焦和相位匹配参数,hBK是Boyd-Kleinman系数,ε0是真空介电常数,deff是准相位匹配的非线性系数。
结果讨论:如图所示是晶体的线性热膨胀系数曲线,数据拟合基本是线性关系
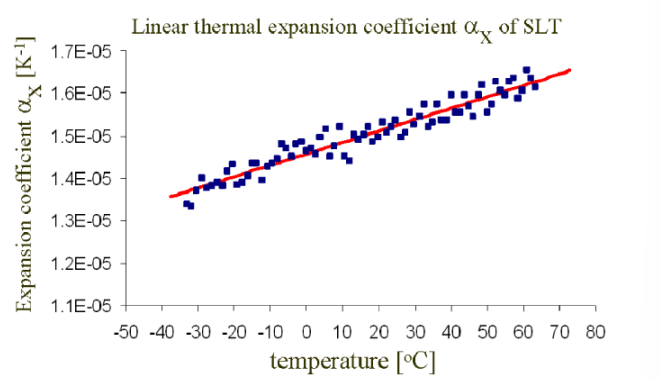
归一化的热光系数线性拟合的参数如表,根据公式β=a0+a1T。
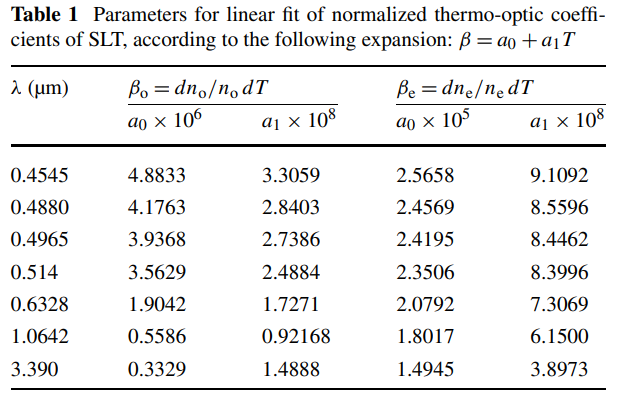
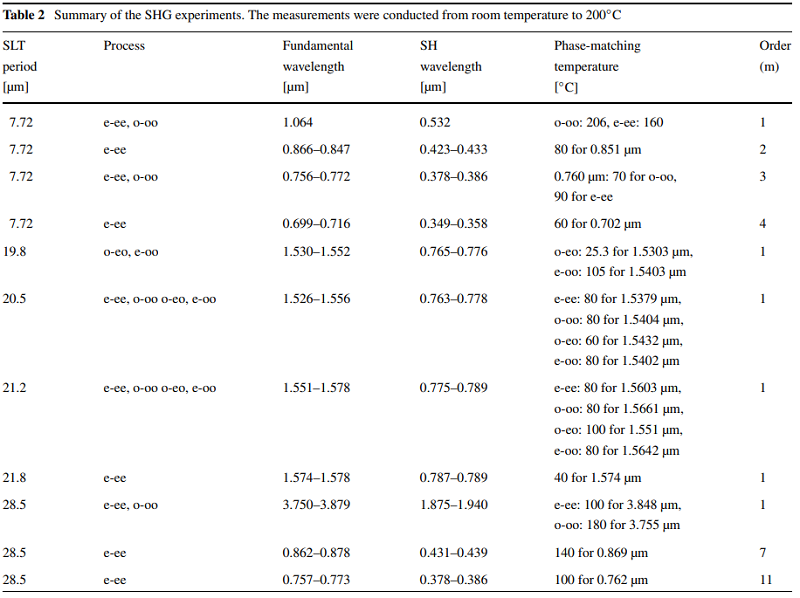
Sellmeier方程的实验数据如表2所示
二阶电极化张量元素测量:测试了固定温度下二次谐波功率对泵浦波长的曲线,以及固定波长下二次谐波对晶体温度的曲线(在所有准相位匹配模式下)
我们还比较了新的ne(λ,T)方程与以前发表的实验结果,包括近红外和中红外OPO光谱。在所有情况下,新方程与实验结果高度吻合。比较了不同的n(λ,T)方程与我们的二次谐波测量结果。对于21.2 um的晶体周期,给出了每个温度下的相位匹配波长,并与根据新方程和Abedin等人的方程计算的理论曲线进行了比较,新的方程与我们的SHG结果非常吻合,而以前发表的方程与我们的实验数据有显著偏差。o-eo和e-oo的 SHG测量包含和,因此交叉验证了Sellmeier方程。o-eo和e-oo测量分别如图所示。新的方程与我们的SHG结果非常吻合。从以前发表的作品中获得的方程与我们的实验观察明显偏离。值得注意的是,尽管NTOC的测量仅限于-30°C-+80°C的温度范围内,但从高温SHG测量中可以看出,它们的色散至少在200°C以上也是有效的。对于e-ee、o-oo、e-oo和o-eo相互作用,晶体21.2um极化周期的SH功率的半高全宽分别为7°C、14°℃、1.2°C和2℃。这些结果表明,与e-ee和o-oo相互作用相比,寻常光和非常光的折射率相互作用对温度的依赖性要强得多。
在这项工作中,我们提出掺杂0.5% MgO 的化学计量LiTaO3 晶体波长和温度依赖折射率方程,掺杂0.5% MgO 的化学计量 LiTaO3缩写是PPMgSLT。我们从准相位匹配频率转换中获得了新的Sellmeier系数,以及利用干涉测量法获得了热膨胀和热扩散系数。 我们新的非常光折射率Sellmeier方程与以前发表的数据以及我们自己的实验结果一致。我们提出了一个新的寻常光折射率方程,它与我们的实验结果十分吻合。o-eo和e-oo 相互作用的测量结果,包括寻常光和非常光的折射率对新方程进行了交叉验证。非常光的掺杂0.5%氧化镁的SLT的ne(λ,T)方程在0.35-6µm光谱范围和25-200◦C温度范围内有效。由于数据不足,我们无法测试全光谱和热范围的寻常光方程的有效性。因此,我们认为折射率Sellmeier方程在波长为0.375-3.75µm和温度范围25-200℃是可靠的。我们还为d33、d22和d24元素的下限值,并推导出它们的比值。我们发现,oeo和e-oo的相互作用与o-oo和e-ee的相互作用相比,在很大程度上取决于晶体温度。推导出的线性和非线性正系数应该有助于基于MgO掺杂SLT中任何二阶相互作用的非线性光学器件的设计。
深圳海纳光学代理进口光学晶体,激光晶体和非线性晶体,支持多种参数的定制,欢迎各位科研工作者前来选购。