作者:海纳光学 时间:2018-12-20
可饱和吸收镜(SAM)一般用于产生短脉冲激光,是一种被动锁模器件。由于其结构简单、安装方便,目前已经广泛应用于产生超短脉冲。可饱和吸收镜的英文名称为Saturable absorption mirror,简称SAM。
可饱和吸收镜的材料主要有染料、吸收晶体和半导体,半导体可饱和吸收镜(SESAM)具有价格便宜、损伤阈值高,输出脉宽段等特点,在于其它材料的竞争中脱颖而出,成为市场主流的可饱和吸收镜。
SESAM半导体可饱和吸收镜是由可饱和吸收体(SA)和反射镜组成,其中反射镜的单晶层和吸收体SA都生长在GaAs晶片上,即下图的粉红色基底上。可饱和吸收镜的原理如下:SESAM可用于宽光谱激光腔,激光在腔内震荡时会一直通过通过可饱和吸收体SA,可饱和吸收体对光的吸收系数随入射光强增大而减小,当吸收达到饱和时则停止吸收并发射脉冲。这个过程也可以描述可饱和吸收镜在弱光情况下吸收并积蓄能量,而在强光状况下光学损耗变小,透射率增大,达到“饱和”状态,SESAM半导体可饱和吸收镜可以瞬间释放所吸收的能量。利用这种饱和吸收特性能够实现对激光的调Q锁模,实现皮秒甚至飞秒量级的超短脉冲输出。使用半导体可饱和吸收镜(SESAM)的被动锁模二极管泵浦固体激光器(DPSS Laser)具有脉冲重复率非常稳定和自启动的特点。

半导体可饱和吸收镜可用于800nm至3μm的宽光谱波长的固态或光纤激光器中。SESAM还可作为非线性光学装置来实现Q开关微芯片激光器。
SAM可饱和吸收镜的主要参数:
半导体可饱和吸收镜主要由布拉格反射镜和可饱和吸收体组成,布拉格反射镜附在GaAs晶圆基底上,而可饱和吸收体位于反射镜上。SAM可以根据不同的应用而设计,例如:不同激光器的损耗,增益谱,腔内功率不尽相同,而可饱和吸收体的参数也要跟这些参数相匹配。
海纳光学代理的德国BATOP公司推出了数百种型号的可饱和吸收镜,它们对应不同的波长、吸收率、脉宽和封装,为用户提供丰富的选择。
SAM可饱和吸收镜的主要参数如下。后文将逐一对这些可饱和吸收镜的关键参数进行介绍
- 吸收率: A - 调制深度:R - 弛豫时间:τ - 饱和通量:Fsat - 吸收体温度
1. Time dependent absorption(吸收率A)
我们将可饱和吸收镜视为两个部分系统:价带和导带。半导体吸收材料的价带中的电子处于基态,当能量E = h·ν的光子被吸收时,会被激发到导带中。如果价带中的状态数是Nv,在导带中为Nc,那么在吸收体的照射期间,两种状态之间的转变率可以描述为:
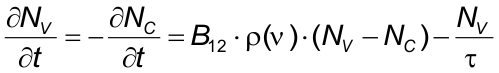
• NV —— 价带中的状态数
• NC —— 导带中的状态数
• B12 = B21 —— 爱因斯坦B系数
• ρ(ν)—— 入射光子的密度
• τ—— 导带中受激电子的弛豫时间。
导带中的受激电子通过自发光子发射或通过非辐射能量损失,以平均弛豫时间常数τ来释放。价带和导带中的状态之和,即吸收过程中发生的电子NT的总数为:NT = NV + NC。
在没有吸收体的照射的情况下,所有电子都处于基态NC = NT。在入射光子密度非常高的情况下,接近激发态NC = NV = NT / 2的最大值,这时对应可饱和吸收镜是透明的。
可饱和吸收体的吸收A与基态的电子数NC成比例。如果我们认为入射光子密度与时间相关的光束强度I(t)成比例,那么我们可以将状态数的速率方程重写为吸收A(t)的速率方程。

• A0 - 非饱和吸收,如果NC = NT / li>
• I(t) - 时间相关的光束强度/ li>
• Fsat = I(t)/(B12ρ(ν)) - 吸收器的饱和通量。
• A(t) - 时间依赖性吸收
我们可以求得该可饱和吸收镜的吸收率A(t)的微分方程的任意解,其中A(t)是与时间有关的吸收率。由于光脉冲强度I(t)本身有一定时间依赖性,可以执行指数函数中的积分。在高斯脉冲的情况下,可以执行指数函数中的积分,从而产生以下依赖于时间的吸收A(t)表达式
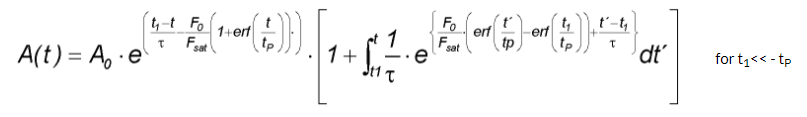
• F0 - 脉冲通量
• tP - 脉冲持续时间。
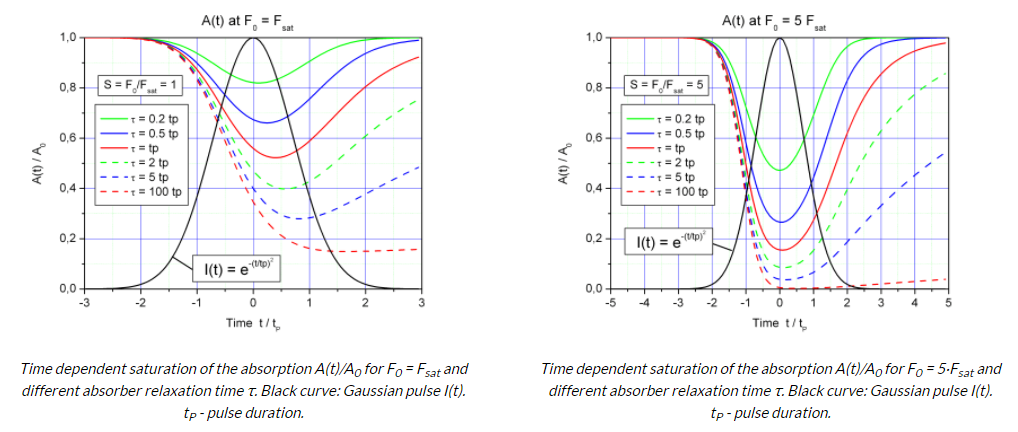
图1为:吸收A(t)/ A0的时间依赖性饱和度对于F0 = Fsat和不同的吸收器弛豫时间τ。黑色曲线:高斯脉冲I(t)。tP-脉冲持续时间;图2为:吸收A(t)/ A0的时间依赖性饱和度对于F0 = 5·Fsat和不同的吸收器弛豫时间τ。黑色曲线:高斯脉冲I(t)。tP -脉冲持续时间
饱和曲线A(F)可以用上面的等式A(t)计算一个确定的时间,例如在脉冲最大值。S = F0 / Fsat是饱和度参数。对于不同的缓冲区弛豫时间/ tau,吸收率A的饱和度; 在脉冲最大值的固定时间t = 0。在吸收器弛豫时间短τ<< tP的情况下,吸收器的调制深度显着降低。
长弛豫时间近似,τ>> tP
在这种情况下,吸收速率方程中的弛豫项可以忽略不计,可获得不同饱和度参数S = F0 / Fsat的时间相关吸收A(t)/A0。
对于t >> tP,我们在上述条件τ>> tP下得到以下饱和曲线。A = A0·e-S (蓝色曲线)的饱和曲线A(S)/A0和近似值A = A0/(1+S)(红色曲线)。
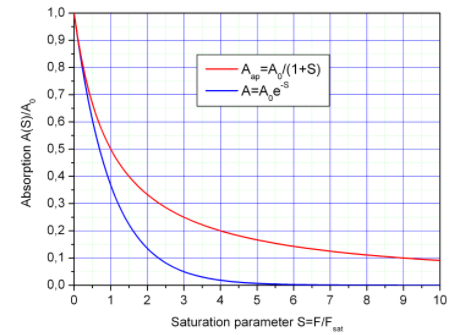
短弛豫时间近似,τ<< tP的近似
在这种情况下,吸收A的上述速率方程中的相关性dA / dt可以忽略,因为每次吸收仅由实际光强度I(t)确定而不是由其历史确定。

有效饱和度通过比率τ/ tP降低。 对于使用可饱和吸收器作为模式锁定器,必须避免这种情况,因为此时调制深度减小。
2. Spatial averaged saturation(空间平均饱和度)
高斯光束的脉冲能量密度取决于距光束轴的距离r(r = 0),影响参数包括:F(r) - 脉冲通量的径向依赖性,r - 到光束轴的距离,F0 - 光束轴上的脉冲能量密度,r0 - 光束半径。
我们考虑缓慢吸收弛豫的情况τ>>tP(τ-激发电子的弛豫时间,tP-脉冲持续时间)。 可以通过计算高斯光束上的空间平均吸收,使用饱和度参数S = F0 / Fsat得到上述平均的结果。
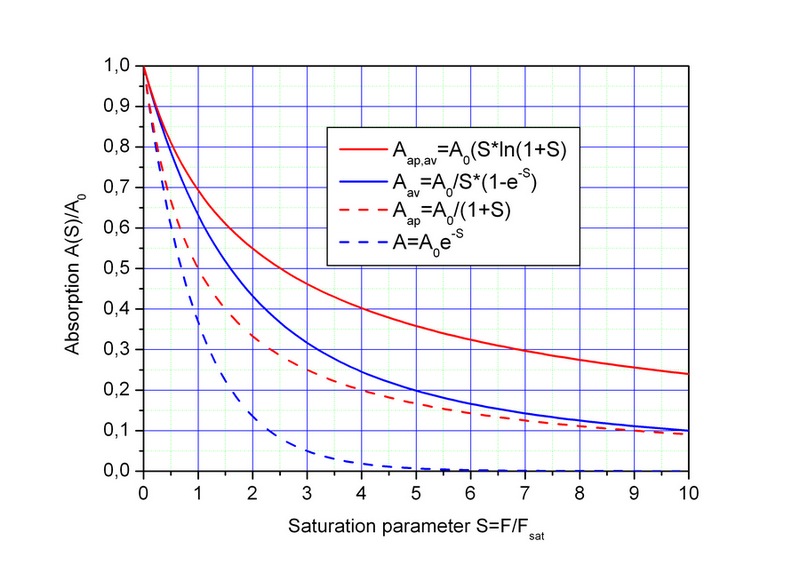
对于速率方程(蓝色)和近似(红色)的精确解,吸收A(S)的非饱和(虚线曲线)和平均(全曲线)的饱和度。高斯光束上的空间平均导致调制深度的减小,如不可饱和的吸收。
3. TPA - Two Photon Absorption(双光子吸收)
在短脉冲的情况下必须考虑两个光子吸收,特别是如果脉冲持续时间tP <1ps。
双光子吸收ATPA增加总吸收如下:
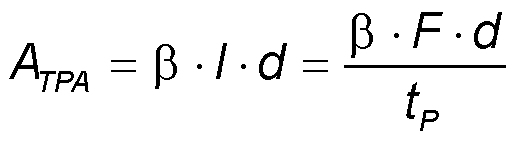
• β - two-photon absorption coefficient 双光子吸收系数
• I - pulse intensity 脉冲强度
• d - absorber layer thickness 吸收层厚度
• F - pulse fluence 脉冲通量
• tP - pulse duration. 脉冲持续时间
时间相关强度I(t)与脉冲持续时间tP的积分导致脉冲能量密度F。因此脉冲能量密度可近似为F~I·tP。
双光子吸收系数β是材料相关参数。对于GaAs材料,β= 2.5•10-10 m / W.
4. Ans - non-saturable absorption(不饱和吸收)
测量不可饱和吸收的主要原因是双光子吸收(TPA),主要是在短脉冲的情况下。
但是,以下两种效应也会导致测量吸收的类似增加:
在饱和度测量期间,吸收剂材料的温度随着脉冲通量的增加而增加。这可能导致增加的测量吸收和增加的脉冲能量密度,但它是次要效应而不是真正不可饱和的吸收。
如果饱和度测量中的脉冲持续时间长于吸收剂材料的最短弛豫时间,则获得“不可饱和”的吸收量。但这仅仅是测量脉冲太长而非真正不可饱和吸收的结果。
如果TPA在短脉冲的情况下是相关的,那么与脉冲持续时间tP相比,吸收器弛豫时间τ也将是大的。这意味着τ>> tP,并且可以使用上述空间平均可饱和吸收的公式A = A0 / S·(1-e-S)。那么积分通量吸收可以写成可饱和吸收和TPA的总和:
• F - pulse fluence脉冲通量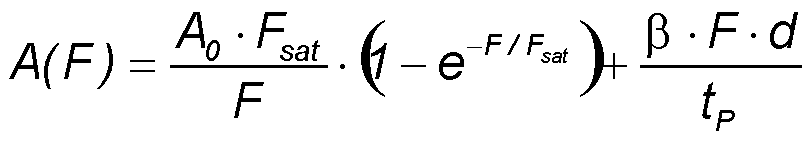
• A0 - low intensity absorption 吸低强度吸收率
• Fsat - saturation fluence吸收材料的饱和吸收通量
• β - two-photon absorption coefficient双光子吸收系数
• d - absorber layer thickness吸收层厚度
• tP - pulse duration. 脉冲持续时间

上图显示了TPA如何在短脉冲的情况下产生不可饱和的吸收Ans。随着脉冲持续时间tP <7sub <的减小,不可饱和吸收增加。
A0 =ΔA+ Ans
TPA有助于稳定短脉冲激光器中的连续波锁模,因为它限制了最大脉冲能量并将Q开关模式锁定降低到低泵浦功率水平范围。
5. SAM reflectance(调制深度R)
可饱和吸收镜(SAM)在布拉格反射镜的阻带内,没有透射。因此反射率为 r1-a。如果包含双光子吸收(TPA) ,且吸收体弛豫时间τ比脉冲持续时间tP短,则可计算 SAM 反射率 r 的横向平均饱和度:
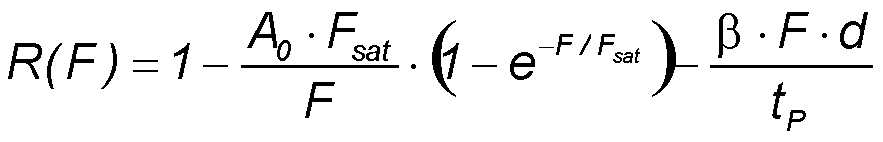
• A0--低强度吸收
• F - 脉冲通量
• Fsat - 饱和度注量
• β - 双光子吸收系数
• d - 吸收层厚度
• tP - 脉冲持续时间。
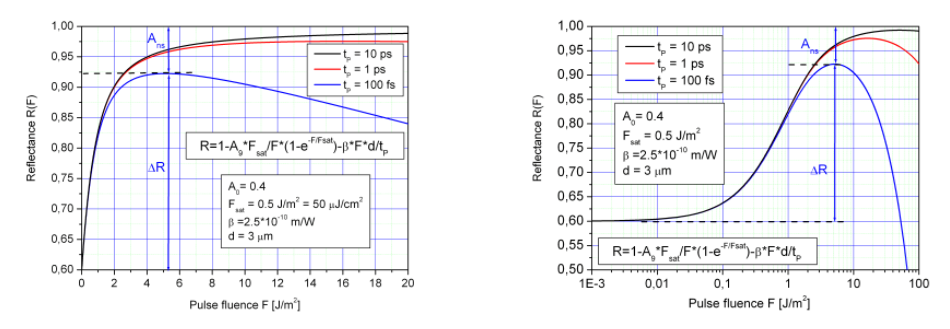
下图显示了SAM的反射率,其中A0 = 0.4,Fsat = 0.5J / m²,吸收剂厚度d =3μm,作为脉冲能量密度F的函数,对于线性和对数标度的三个不同脉冲持续时间tP。
由于吸收器和布拉格反射镜中的TPA(双光子吸收),调制深度ΔR小于低强度吸收A0并且取决于脉冲持续时间。TPA系数β取决于材料。 它随着半导体材料能隙的减小而增加,并且只能由于吸收层和布拉格反射镜中的不同材料而估计
6. elaxation time τ(弛豫时间τ)
可饱和吸收层由半导体材料组成,其直接带隙略小于激光束的光子能量。光照被吸收时,在吸收膜中产生了电子-空穴对。对于锁模激光器,激发载流子的弛豫时间应略长于脉冲宽度。在这种情况下,脉冲后沿是不被吸收的,但在两个连续的脉冲之间的空档,饱和吸收体又会恢复到非饱和状态对下一个脉冲进行同样的调制。
由于直接半导体中自发光子发射的弛豫时间约为1 ns,因此为了实现锁模,必须采取一些措施来缩短弛豫时间。这就需要给饱和吸收层中引入晶格缺陷使载流子进行非辐射弛豫,SESAM主要基于以下技术:
1)低温分子束外延技术(LT-MBE)
2)正离子注入技术。
两种技术的关键参数都是生长温度。一般而言,SAMs弛豫时间的典型值在500fs 到30ps 之间。
泵浦-探测测量的弛豫时间τ如下图所示:

7. Saturation fluence(饱和通量 Fsat)
饱和通量 Fsat 取决于半导体材料和 可饱和吸收镜SAM 的光学设计。 低饱和通量的优点是可以在低功耗下启动激光锁模。这样就避免SAM在强光下不被损伤且功能不会减退
为了减小饱和通量,半导体吸收层的厚度减小到10nm以。这种情况下,垂直于SAM吸收层会发生电子能量和动量的量子化现象,这也会造成态密度降低到致密半导体的值以下。所以SAM中的饱和吸收层可以看作是一个带隙比两边小的量子阱。如果SAM需要一个更大的吸收光通量,则需要增加量子阱的数量,而不是使用单一的厚吸收层。
SAM中布拉格反射镜前面的电场强度,是一个拥有节点和腹点的周期性的函数。吸收层量子阱的位置一般处于腹点处从而可以获得一个低的饱和通量值。布拉格反射镜和半导体-空气界面的菲涅尔反射一起构成了一个类似于法布里-珀罗的谐振器,其中包含有量子阱。这两个反射层之间的半导体厚度决定了腔内会形成谐振或者反谐振。由于腔内场的增强,谐振 SAM 的饱和通量比反谐振 SAM 的饱和通量低。
共振 SAM 的典型饱和通量为 Fsat ~ 30μJ/cm²=0.3μJ/m²,
反共振 SAM 的饱和通量为 Fsat ~ 120μJ/cm²=1.2μJ/m²。
8. Influence of absorber temperature(吸收体温度的影响)
SAM的参数会受其温度的影响,体现在两个方面: 吸收材料的热膨胀 和 半导体带隙随温度的升高而减小。
与温度有关的光深度ot
第二种效应导致折射率 n + i k 随着温度的升高而增加。随着温度的升高,热膨胀导致光深度d增加(实际部分折射率,d 膜厚度)。 因此,随着温度的升高,SAM 的光谱反射曲线向长波方向移动。 这种热位移可以在典型的由AlAs、 GaAs 和 InGaAs 组成的 SAM 中测量到。可以确定光学厚度的温度系数αot ~ 7×10-5/K.
这个值比 GaAs 的线性热膨胀系数αt = 5.39×10-6 / k 要大得多,因此主要取决于带隙和折射率的变化。利用这一关系式可以计算 SAM 光谱曲线的温度漂移,公式为:
n·d(T) = n·d(T0 + ΔT) = n·d(T0) · (1 + αot · ΔT) or Δ(n·d) = n·d(T0) · αot · ΔT
• n·d - optical thickness 镜片厚度
• T0 - reference temperature参考温度
• ΔT = T - T0 - temperature difference温差
• αot - temperature coefficient for optical thickness镜片厚度的温度系数
• Δ(n·d) - optical thickness difference. 镜片厚度差
温度上升100 K使SAM光谱曲线在1μm波长处向更长波长移动7nm,在3μm处移动21nm。 在共振SAM的情况下,这种偏移很重要。
吸收温度依赖性
折射率的虚部 k,半导体的直接吸收随温度的升高而增加。这也是随着温度的升高带隙减小的结果。对于一个典型的SAM 来说,想象部分k的温度系数/折射率是αk ~ 6×10-3/K。用这个系数可以计算出k的温度依赖值:
• k(T) = k(T0)·(1+αk·ΔT)
因此,当吸收剂温度提高83k时,吸收系数k和吸收系数SAM 增加50%。这种温度依赖性对激光锁模有重要影响。
9. Absorber temperature(吸收体温度)
可饱和吸收体将一部分入射光子能量转化为热能。这种热能在光脉冲产生期间和产生后不久提高了吸收层的温度。 之后,热量通过基体传输到基体后侧的散热基底。比如GaAs基底,其具有很好的高导热率,即使有微不足道的散热量也会通过表面散热到空气中。
在脉冲激光作用下,吸收体温度 t 会随着脉冲重复频率呈周期性变化。 从吸收层到散热器的连续热流,会产生恒定的吸收体温度上升量ΔTstat。最大的吸收体的温度上升量ΔTmax可以通过时间相关动态部分ΔTdyn(τ+ tp)和静态部分ΔTstat之和来描述。其中重要的参数有脉冲宽度tp和饱和吸收体中的载流子弛豫时间τ
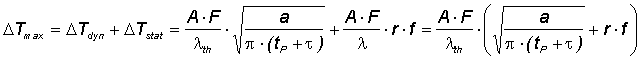
• T 温度上升量
• A 吸收率
• F 脉冲通量
• λth 吸收材料热导系数 (55W/mK for GaAs)
• a 吸收材料热扩散率 (3.1×10-5m²/s for GaAs)
• tp 光脉冲宽度
• T 吸收体载流子弛豫时间
• r 吸收体上的光斑半径
• f 光脉冲重复频率
下面的两幅图表示的是,静态温度上升ΔTstat和光斑的半径r的关系,和动态温升ΔTdyn与吸收体中载流子弛豫时间的关系的函数。结果显示,固态激光器中(吸收A = 0.03),而光纤激光器(吸收A=0.3)。
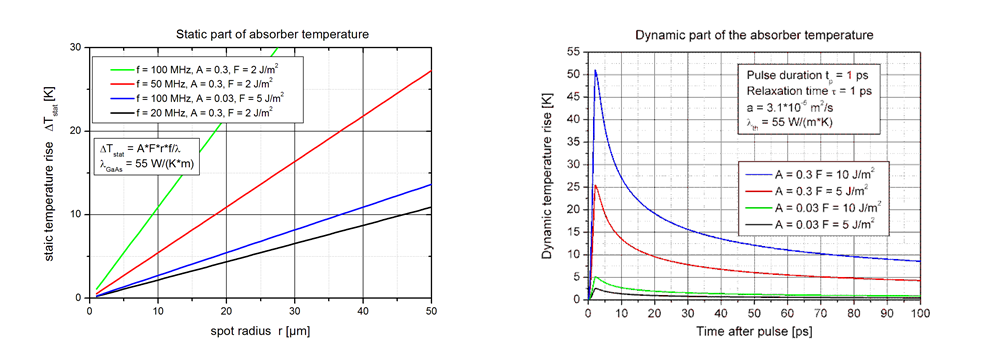
随着吸收器弛豫时间τ的增加,最大温度上升减小,因为在弛豫时间之后吸收的能量从被激发的电子释放到晶格中。 如果弛豫时间τ比脉冲持续时间tp长,则电子在短时间内存储吸收的能量,而热能已经从吸收层扩散到基底中。
10.Dispersion 分散
可饱和吸收镜由一个布拉格反射镜和一个前面有一定光深度的吸收层(n·d)组成。半导体吸收体和空气之间的接口构成了第二个菲涅耳反射器。 SAM的吸收和分散取决于下列参数:
表面反射率Rs
光学吸收剂厚度n•d
吸收系数α。
Anti-resonant SAM(反共振SAM)
如果 SAM 涂有抗反射(AR)涂层(Rs=0) ,那么光束仅反射在布拉格反射镜上。这导致了一个类似于介质镜的小分散体。
反共振SAM-1040-2-1ps的群速度色散(GVD)。
使用反射相的二阶导数计算GVD。
对于反共振SAM,GVD在阻带的光谱区域中很小。
Resonant SAM(共振SAM)
如果吸收层被封闭在由布拉格反射镜和Rs> 0的表面反射镜确定的空腔中,则光在两个反射镜上部分反射。 以下两种效应决定了净反射率和色散:
吸收层的光学厚度n•d。
吸收材料的吸收系数α。
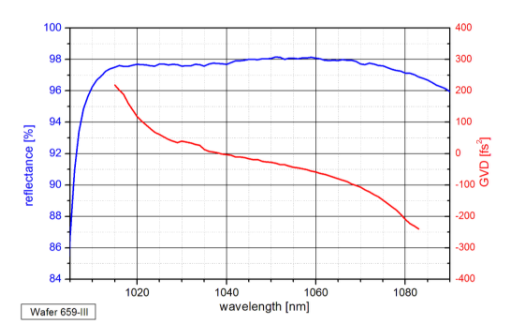
共振SAM-1030-32-3ps的群速度色散(GVD)。
使用反射相的二阶导数计算GVD。
最大吸收和最低反射率在共振波长λ= 2•n•d。 在该共振附近,GVD快速变化,而在共振之外,GVD缓慢变化。
共振附近的GVD变化的幅度随着光学厚度n·d的增加和吸收层的吸收系数α的减小而增加。